Publications de Jean-Yves BOULAY

Jean-Yves Boulay

 Listing of some pre-print papers about genetic code, number theory, quantum physics and connections between all these research fields:

Amino acid numbering, ultimate numbers and the 3/2 ratio

October 2022       DOI: 10.13140/RG.2.2.17690.93128

An unprecedented numbering of the twenty proteinogenic amino acids, itself deduced from a logical numbering of the sixty-four DNA triplets, reveals connections between the mechanism of the genetic code, of the field of Biology, and the number theory field, of which more precisely the notion of ultimate number, one of the four classes of Mathematics entities proposed to constitute the set of whole numbers. These connections are revealed in an physico-arithmetic organization of the genetic code in various ratios of 3/2 value as global configurations.

Numbering of the twenty proteinogenic amino acids

September 2022 DOI: 10.13140/RG.2.2.13001.83046/1

By proposing a numbering of the twenty proteinogenic amino acids deduced from the physicochemical properties of the four coding DNA nucleobases, it is established that this amino acid number, equal to 5x entities, is not arbitrary. Indeed, we demonstrate that many attributes of these twenty amino acids, as a whole, are also 5x in number and that by isolating, since their numbering, the 3x peripheral amino acids from the 2x internal ones, these attributes are divided into ratios of 3/2 as exact value. This is verified both as the physicochemical properties of the 20 amino acids and as the coding configurations of the nucleobases, the source of this numbering.

Stealthy orbitals hypothesis

November 2021  DOI: 10.13140/RG.2.2.19410.07365/1

The graphic charting of atomic orbitals into the form of chevrons suggests the existence of stealth orbitals occupying the quantum vacant space of the various electronic shells. It is proposed here, the hypothesis that these quantum gates allow transit of electrons from orbital to another, and that these gates can be accesses to quantum singularities without space-time. Singular arithmetic arrangements in the distribution of real and stealthy orbitals of certain genetic code components reinforces the hypothesis to existence of these quantum gates.

The atomic orbitals quantum charts into chevron form

November 2021  DOI: 10.13140/RG.2.2.12643.48161

It is proposed here to represent the quantum distribution of atomic orbitals in an unprecedented table where the quantum shells and subshells are drawn in the form of chevrons whose vertices are occupied by orbitals with the magnetic quantum number m = 0. This new representation visually shows, much better than a classic linear chart, the relationship between the number of quantum shells and the number of orbitals. Also, this new visual model can be easily used in the individual quantum depiction of the atoms represented alone or into molecules and can find its place in illustration of some two-dimensional space-time quantum theories.

Chevron Form Quantum Charts

November 2020  DOI: 10.13140/RG.2.2.35925.45283

It is proposed here to represent the quantum distribution of atomic orbitals in an unprecedented table where the quantum shells and subshells are drawn in the form of chevrons whose vertices are occupied by orbitals with the magnetic quantum number m = 0. This new representation visually shows, much better than a classic linear chart, the relationship between the number of quantum shells and the number of orbitals. Also, this new visual model can be easily used in the individual quantum depiction of the atoms represented alone or into molecules and can find its place in illustration of some two-dimensional space-time quantum theories. Finally, this graphic representation allows to introduce the hypothesis of the existence of stealth orbitals, quantum gates opening towards singularities.

Genetic code, quantum physics and the 3/2 ratio

July 2020              DOI: 10.13140/RG.2.2.26505.67681/3

 The analysis of the quantum structure of the five chemical elements composing the coded twenty amino acids and the four coding nucleotides of DNA working in the organization of the genetic code reveals an opposition of their respective constituents in always an arithmetic ratio of value 3/2 according to the parity of the number of their quantum shells. Also, the quantum analysis of the amino acid Glycine, the smallest component of peptides that can be confused with saturated base, reveals the same arithmetic oppositions of 3/2 value of its components by the differentiation, operated according to their number of protons, of its five chemical groups. . In sidelines to this study, a new graphic representation of the chemical elements is introduced: chevron form quantum chart.

New Whole Numbers Classification

June 2020            DOI: 10.13140/RG.2.2.26139.90402/2

According to new mathematical definitions, the set (ℕ) of whole numbers is subdivided into four subsets (classes of numbers), one of which is the fusion of the sequence of prime numbers and numbers zero and one. This subset, at the first level of complexity, is called the set of ultimate numbers. Three other subsets, of progressive level of complexity, are defined since the initial definition isolating the ultimate numbers and the non-ultimate numbers inside the set ℕ. The interactivity of these four classes of whole numbers generates singular arithmetic arrangements in their initial distribution, including exact 3/2 or 1/1 value ratios.

The ultimate numbers and the 3/2 ratio

March 2020          DOI: 10.13140/RG.2.2.32843.34081/3

According to a new mathematical definition, whole numbers are divided into two sets, one of which is the merger of the sequence of prime numbers and numbers zero and one. Three other definitions, deduced from this first, subdivide the set of whole numbers into four classes of numbers with own and unique arithmetic properties. The geometric distribution of these different types of whole numbers, in various closed matrices, is organized into exact value ratios to 3/2 or 1/1.

Pi and Golden Number: not random occurrences of the ten digits

September 2019 DOI: 10.13140/RG.2.2.20762.57287

This paper demonstrates that the order of first appearance of the ten digits of the decimal system in the two most fundamental mathematical constants such as the number Pi and the Golden Number is not random but part of a arithmetical logic. This arithmetical logic is identical to Pi to its inverse and to the Golden Number. The same arithmetical phenomenon also operates in many other constants whose square roots of numbers 2, 3 and 5, the first three prime numbers.

 Jean-Yves Boulay

Researcher profile of Jean-Yves Boulay on Researchgate.net

Numbering of the twenty proteinogenic amino acids

3/2 ratios inside the genetic code

Abstract

By proposing a numbering of the twenty proteinogenic amino acids deduced from the physicochemical properties of the four coding DNA nucleobases, it is established that this amino acid number, equal to 5x entities, is not arbitrary. Indeed, we demonstrate that many attributes of these twenty amino acids, as a whole, are also 5x in number and that by isolating, since their numbering, the 3x peripheral amino acids from the 2x internal ones, these attributes are divided into ratios of 3/2 as exact value. This is verified both as the physicochemical properties of the 20 amino acids and as the coding configurations of the nucleobases, the source of this numbering.

Conventional nomenclature and alphanumeric symbol proposal to the twenty proteinogenic amino acids into 5 characters: 2 digits + 3 letters.

complete paper: Numbering of the twenty proteinogenic amino acids

 Jean-Yves BOULAY independent researcher (without affiliation) – FRANCE –

 jean-yvesboulay@orange.fr  ORCID: 0000-0001-5636-2375

Amino acid numbering, ultimate numbers and the 3/2 ratio

Connections between genetic code and number theory

Jean-Yves Boulay

Abstract. An unprecedented numbering of the twenty proteinogenic amino acids, itself deduced from a logical numbering of the sixty-four DNA triplets, reveals connections between the mechanism of the genetic code, of the field of Biology, and the number theory field, of which more precisely the notion of ultimate number, one of the four classes of Mathematics entities proposed to constitute the set of whole numbers. These connections are revealed in an physico-arithmetic organization of the genetic code in various ratios of 3/2 value as global configurations.

 complete paper: Amino acid numbering, ultimate numbers and the 3/2 ratio

References

1. Jean-Yves Boulay. The ultimate numbers and the 3/2 ratio. 2020. ⟨hal-02508414v2⟩ DOI: 10.13140/RG.2.2.32843.34081/3

2. Jean-Yves Boulay. New Whole Numbers Classification. 2020. ⟨hal-02867134⟩ DOI: 10.13140/RG.2.2.26139.90402/2

3. Jean-Yves Boulay. Numbering of the twenty proteinogenic amino acids. 2022. DOI: 10.13140/RG.2.2.13001.83046/1

4. Sergey Petoukhov. Genetic Code and the Ancient Chinese Book Of Changes. Symmetry: Culture and Science Vol. 10, Nos. 3-4, p. 211-226. 1999.

Jean-Yves BOULAY independent researcher (without affiliation) – FRANCE –

 jean-yvesboulay@orange.fr  ORCID: 0000-0001-5636-2375

Chevron Form Quantum Charts

New graphical representation of quantum orbitals 

Jean-Yves Boulay

Abstract. It is proposed here to represent the quantum distribution of atomic orbitals in an unprecedented table where the quantum shells and subshells are drawn in the form of chevrons whose vertices are occupied by orbitals with the magnetic quantum number m = 0. This new representation visually shows, much better than a classic linear chart, the relationship between the number of quantum shells and the number of orbitals . Also, this new visual model can be easily used in the individual quantum depiction of the atoms represented alone or into molecules and can find its place in illustration of some two-dimensional space-time quantum theories. Finally, this graphic representation allows to introduce the hypothesis of the existence of stealth orbitals, quantum gates opening towards singularities.

1. Introduction

In the scientific quantum literature, many tables already exist describing the quantum structure of matter. Very often, these tables are represented in the same general linear form to describe the distribution of orbitals and electrons on the different quantum shells of chemical elements. The quantum study of the genetic code [1] has was an opportunity to propose a new type of table describing the quantum organization of atoms. We will demonstrate here, after having compared it to a classical illustration, that this new concept of chart, using an innovative representation of quantum shells arranged in the form of chevrons is more explicit in the study of chemical elements and molecular chemical structures.

2. Linear chart versus chevron form quantum chart

2.1 Classical linear quantum chart

In Figure 1 is illustrated a classical quantum table of linear form of the first three shells and the first six quantum subshells. This type of table is conventionally used in quantum scientific literature.

 Fig.1 Classical linear quantum chart of the first three shells and the first six subshells. See Fig.2 to comparison.

In this linear form chart, the relationship between the shell number and the orbital amount is not clear. Visually, by shell, we need to add each orbital line to understand that their sum is equal to the square power of the shell number.

 - 1^st shell →           1 orbital = 1² = 1 orbital,

- 2^nd shell →          1 + 3 orbitals = 2² = 4 orbitals,

- 3^rd shell →          1 + 3 + 5 orbitals = 3² = 9 orbitals.

Note: Here it is the quantum number mℓ which is the subject of study. For graphic simplification this value is simply noted m in the demonstrations.

2.2 New chevron form quantum charts

In figure 2 is illustrated the new concept of quantum chart in chevron form. Inside this table, the different quantum shells and subshells are so presented in the form of chevrons.

At the top end of each rafter are indicated the names of the different shells and subsells; at the left end of these chevrons, the numbers of orbitals and electrons of these different shells and quantum subshells are indicated. At each chevron vertex is the orbital where the quantum number m = 0. The orbitals with positive quantum number m are progressively positioned towards the top of these chevron vertices and the orbitals with negative quantum number m are progressively positioned towards the outside left of these chevron vertices.

 Fig. 2 New chevron form quantum chart: quantum distribution of orbitals and electrons in the first three shells and the first six subshells. See Fig.1 to comparison.

This new graphic design is more explicit in describing the quantum structure of chemical elements than any other usual linear chart. Very visually, as illustrated Figure 3, this chevron configuration clearly highlights the arithmetic progression of the orbital numbers of the different quantum shells in square powers of the level of these electronic shells.

Fig. 3 Square geometric correspondences between shell quantum number and number of orbitals.

2.3 Classical versus chevron form quantum chart

Figure 4 can would be without from comment. Compared to the classic version, the chevron form version of the quantum chart brings a vision as in relief of quantum shells (See Chapter 3.1). In this new version, for each quantum shell, the orbitals appear as a compact square block whose dimension is directly proportional to the shell number (square power). Also, orbitals with the same magnetic quantum number (m) are arranged on the same diagonals. All of this is instantly visible in this chevron-shaped version, unlike the linear classic version.

 Fig. 4 Classical chart versus chevron form quantum chart.

3 General chevron form quantum chart

Figure 5 shows the chevron form quantum table of the first 15 electronic shells. This graphic concept is extensive development of that introduced in Chapter 2.1 and illustrated in Figure 2. We suggest that this new graphic type be favoured for the description of the quantum organization of the different chemical elements.

 Fig. 5 General chevron form quantum chart representing the first 5 shells and first 15 quantum subshells of the chemical elements. Distribution of orbitals and electrons in these shells and subshells.

3.1 Chevron form quantum chart appellation

Although it is two-dimensional, this new type of graphics gives a three-dimensional aspect of the quantum structure of the elements. It is for this reason that the term "form" is preferred to that of "shape" in the name of this new chart concept. Nevertheless, this chevron form chart representation can find its place in illustration of some two-dimensional space-time quantum theories.

3.2 Chevron form quantum chart why electron spin

In this introduction to the new graph concept, the spin of the electron has not been detailed in order to lighten the presentation. But of course, this new chevron form quantum chart can also be represented by indicating the values of the spins as illustrated Figure 6.

 Fig. 6 New chevron form quantum chart why detail of electron spin.

The non-value presentation of spins is privileged in the following demonstrations, allowing the distinction of the own electrons from those guest in the quantum description of atoms and molecules.

4. Atoms quantum charts

In this new quantum chart concept, and more generally in the quantum study of the chemical elements [1], the electronic spin is so not detailed (by ascending or descending arrows). In return, it is the migratory or non-migratory nature of the electrons which is highlighted. Thus, for example, representation of the nitrogen atom and sulphur atom such as that illustrated below (Figure 7) is favoured.

 Fig. 7 Graphical quantum representation of Nitrogen and Sulphur in chevron form design (in their saturated state). See also Fig. 2 and Fig. 5.

With this new quantum chart design, the relative dimension of quantum shells and subshells is also more explicitly perceptible than in a line graph (such as the one presented in Figure 1).

In Figure 8 is illustrated, in the new chevron form chart concept, the quantum structure of the first ten chemical elements. This type of table gives simultaneously, visually, a lot of quantum but also physical information, in particular a good idea of the electronic wingspan of the different chemical elements represented.

 Fig. 8 Graphical quantum representation of the first ten atomic elements in chevron form design (in their saturated state). See also Fig. 2 and Fig. 5.

In this table, with this kind of graphic representation, we can clearly see the differences in electronic organization of the three groups of chemical elements isolated according to their number of quantum subshells (here 1, 2 or 3 subshells).

 4.1 Atoms quantum scripting

From the concept of representation of atoms in chevron form quantum chart, we now propose a quantum writing of the chemical elements.

 Fig. 9 Graphical scripting of chemical elements from chevron form quantum charts.

Thus, as illustrated in Figure 9, we propose for example a quantum scripting of the element nitrogen under the form:

N₂)₂)₃)

This type of quantum writing quickly but clearly describes the electronic structure of the element considered with the graphics parentheses separating the different subshells. This quantum scripting is more easily readable that, for example for Nitrogen,  this fastidious classical script:

1s² 2s² 2p³

Also, a variant of this quantum writing can be envisaged with two different sizes of parentheses distinguishing the boundaries of shells and of subshells:

N₂)₂)₃)

In addition, it is possible to consider a simplified variant of this quantum writing of the elements by distinguishing only the shells alone (without showing the subshells):

N₂)₅)

However, in order to clearly introduce this new concept of quantum scripting, we favour the use of the first formula with, for example, scripting N₂)₂)₃) to chemical element Nitrogen.

5. Molecules quantum charts

From the atoms quantum charts in chevron form (see Figures 7 and 8), then we propose a representation of molecules under the aspect of that presented in Figure 10.

 Fig. 10 Quantum structure of Glycine in a chevron form quantum chart. See Fig. 8.

This does not represent molecular orbitals but describes the source orbitals of each atom. Again, the chevron-shaped representation of quantum shells, subshells, orbitals and electrons distributed over them appears clearer than a linear or circular representation of atoms.

6 Stealthy orbitals hypothesis

6.1 Stealthy orbitals concept introduction

This new graphic chevron-shaped representation of the quantum organization of electronic shells is the opportunity to propose the hypothesis of the existence of stealthy orbitals. We therefore propose the existence of two additional stealth orbitals on each end of the quantum subshells, this excepted for the very first subshell 1s. Figure 11 illustrates this concept for chemical elements Nitrogen and Sulphur as example.

 Fig. 11 Graphical quantum representation of Nitrogen and Sulphur in chevron form design (in their saturated state) with highlights of stealthy orbitals. See Fig. 2 and Fig. 5 also.

These stealthy orbitals can be considered as quantum gates where pass electrons changing orbital and subshell, especially in their interatomic migrations.

Although these "quantum gates" graphically (in square shaped) fill the chevrons so as to close the quantum shells, they are not affected by the different quantum numbers applied to the electrons. Any of these gates can be therefore taken by any single electron within a shell.

Beyond and through these quantum gates, the electrons pass through a singularity without classical spacetime and are therefore projected instantly from an orbital to another (outside or inside atoms).

6.2 Stealthy orbitals concept depiction

Into Figure 12 amino acid Glycine is depicted in its zwitterionic state. This doubly ionized state is a good way to illustrate the different possible configurations of stealth orbitals supposed to operate in the quantum subshells of atoms.

 Fig. 12 Graphical quantum representation of chemical groups NH₃+, CH₂ (alpha carbon) and O- (from COO-) of amino acid Glycine in its zwitterionic state. Own electrons (in black) and guest electrons (in grey).  See Fig. 10 also.

Thus, quantum gates can be into three possible states:

6.3 Stealthy orbitals and singularity

The stealth orbital hypothesis also requires us to propose the existence of singularities where electrons temporarily transit. The latter term is actually not really appropriate since we suggest that in these singularities there is neither time nor space. We therefore call them "singularities without spacetime". These singularities are therefore a virtual place (without space) where electrons pass when they operate in covalent bond. Figures 13 and 14 will now illustrate the quantum mechanism of these virtual entities.

6.3.1 Classical functioning of singularities

When two orbitals are in possible interaction, so stealthy orbitals activate and a singularity appears. In this new stealthy orbitals hypothesis, we suggest that the first orbital 1s is simultaneously also as a quantum gate (stealth orbital) but only when this orbital does is by only one electron, so in fact only for the hydrogen atom.

 Fig. 13 Graphical quantum depiction of three classical covalent bonds using gates and quantum singularity. Own electrons (in black) and guest electrons (in grey). See Fig. 12 also.

6.3.2 Functioning of singularities in ionised configurations

Figure 14 illustrates the interactions between orbitals of the Hydrogen in excess and of Nitrogen in the positively ionized NH3+ group and what happens to the celibate orbital of Oxygen in the negatively ionized COO- group of the zwitterionic Glycine introduced in Figure 12 and used as an example.

 Fig. 14 Graphical quantum depiction of two ionised configurations using gates and quantum singularity in NH3+ group and COO- group of zwitterionic Glycine. See Fig. 12 also. Own electrons (in black) and guest electrons (in grey).

 In positive ionisation, an electron (·+) from Hydrogen atom (thus orbiting on a gate-orbital*) can generate a singularity towards a quantum gate (of a non-hydrogen atom, in the example: Nitrogen). But this one, not being connected to any orbital, stays on its orbital. Nevertheless, a non-binding bond is possible between the two atoms because an electron of Nitrogen atom (from a full orbital) can cross the singularity to join and share the celibate orbital of Hydrogen atom.

In negative ionisation, a celibate electron (·-) fromthe third Oxygen subshell activates a gate and a singularity. But this gate remains semi closed (so, as far as, semi open) and the electron cannot penetrate or cross the singularity because there is not another activated gate (stealth orbital) due to the absence of a Hydrogen atom where it can migrate. So this electron stays on its orbital and none bond is created. However, the non-filling of the orbital in Oxygen, leave open a passage in the singularity and in the quantum gate which therefore remains semi open.

*Recall: it is agreed that, in Hydrogen atom, the first orbital 1s is simultaneously also as a quantum gate (stealth orbital).

6.4 Functioning of singularities

Some way, one can say that various configurations illustrated in Figures 13 and 14 are as molecular orbitals. So, from the stealth orbitals hypothesis, a molecular orbital is structured like this:

 orbital ↔ quantum gate ↔ singularity ↔ quantum gate ↔ orbital

As the light wave is an emanation of the photon, the singularity is an emanation of the celibate electron. Also It is the singularity, emanation of a electron, that activates the gates between celibate electrons. but these quantum gates are not emanations of electrons, they are in a vacuity state.

7 Stealthy orbitals and chevron form quantum chart

The hypothesis of stealth orbitals allows us to offer a more quantum chart trimmed and still in chevron form.

7.1 Chevron form quantum chart including stealth orbital

Figure 15 represents a chevron form quantum chart similar to that previously introduced in Figure 5 Chapter 3. However, this one is enriched with stealthy orbitals (so quantum gates) proposed in hypothesis Chapter 6. 

Fig. 15 Full general chevron form quantum chart representing the first 5 shells and first 15 quantum subshells of the chemical elements. Distribution of orbitals, stealthy orbitals (quantum gates) and electrons in these shells and subshells.

 In this table, all the different quantum shells and subshells are graphically closed in square shaped polygons. This can approach the real physico-quantum configuration of the electronic clouds surrounding atomic nuclei and this, although we perceive them in three dimensions.

7.2 Figurative chevron form quantum chart

In a graphic optimization of the new concept of a quantum chart in chevron form, a concept integrating the hypothesis of the existence of stealth orbitals, we finally propose a figurative representation of the physico-quantum organization of the electronic shells of the different chemical elements.

 Fig. 16 In a figurative shape, general chevron form quantum chart representing the first 5 shells and first 15 quantum subshells of the chemical elements. This, as an abstract of chart in Fig.15.

This intuitive figuration illustrated in Figure 16 opens the debate of new quantum theories towards an idea of a two-dimensional structure of the clouds of electrons surrounding the atomic nuclei. However, in order not to confuse the so already complex notions introduced here, this will not be developed in this paper.

8 Orbitals, stealthy orbitals, genetic code and the 3/2 ratio

The stealth orbital hypothesis is reinforced by the permanence of an arithmetic phenomenon previously revealed in the article "Genetic code, quantum physics and the 3/2 ratio" [1]. In this paper, we have shown that the chemical elements entering into the composition of the different components of the genetic code (amino acids, DNA) are opposed in various ratios of value 3/2 according to multiple criteria.

In overlay of this, the distribution of stealth orbital these genetic components also organizes in various arithmetical ratios of 3/2 value.

8.1 The five chemicals elements of the genetic code

Only five atoms make up the twenty genetically encoded amino acids. These five different atoms distribute their electrons over one, two and three quantum shells. According to these physico-chemical criteria, chart Figure 17, these five atoms are opposed in two groups in a duality of three versus two atoms: Carbon, Nitrogen and Oxygen are with even number of quantum shells; Hydrogen and Sulphur have an odd number of quantum shells. Still in a 3/2 ratio duality, the three atoms with an even number of electron shells total six shells (2 + 2 + 2 = 6 shells) versus four (1 + 3 = 4 shells) for the two atoms with odd number of quantum shells.

 Fig. 17 Differentiation of the 5 atoms constituting 20 amino acids into 2 groups of 3 and 2 atoms according to the parity of their number of electron quantum shells. * In DNA, Phosphorus replaces Sulphur.

DNA is also made up of the same five different qualities of atoms except that Phosphorus replaces Sulphur. However, these last two atoms have the same number of electron shells and the same electronic structure in their saturated state (inside molecules) with the same maximum number of electrons that can orbit their nucleus. So Phosphorus and Sulphur having the same saturated quantum configuration, these two elements can be confused in following demonstrations.

Figure 18 illustrates the quantum structure of the five atoms working in the genetic code. Thus it appears that, both "true" orbitals and "stealth" orbitals (quantum gates) are organized in ratios of 3/2 value in the opposition of the three chemical elements with an even number of quantum shells (C, N and O) to the other two with an odd number of shells (H and S or P for DNA).

 Fig. 18 Quantum structure depiction of the five chemical elements constituting 20 amino acids of genetic code. Arithmetical opposition in 3/2 ratio of true orbitals and stealth orbitals according to the parity of number of electron quantum shells of these elements (In DNA, Phosphorus replaces Sulphur).

 8.2 Glycine and Methionine quantum structure

Into amino acid Glycine, the smallest proteinogenic peptide and into Methionine, the amino acid initiator of peptide chains, true and stealth orbitals (quantum gates) are distributed in singular arithmetic arrangements. These physico-quantum configurations reinforce the likelihood of the existence of these stealth orbitals. Next depictions of these two amino acid will made in isolated molecular state.

8.2.1 Glycine quantum structure

Among the twenty amino acids, Glycine is distinguished by its absence of radical. Its radical is reduced to a simple hydrogen atom which in a way simply closes the base structure common to each amino acid. So Glycine can be considered as a base, more precisely as glycined base. Quantum study of it reveals singular arithmetic arrangements of its true and stealth orbitals (quantum gates). 

 Fig. 19 Quantum structure of Glycine in a chevron form quantum chart: 30 true orbitals whose 10 filled orbitals and 20 semi-full orbitals, 20 stealthy orbitals. 40 own electrons (in black)  and 20 guest electrons (in grey). See Fig. 7 and 8.

The illustration of the detailed quantum structure of Glycine (in isolated molecular state) therefore reveals that number of true orbitals and that of stealthy orbitals are in a ratio of value 3/2. In transcendence to this, another arithmetic phenomenon is revealed. It is also that the total number of stealth orbitals and filled orbitals is equal to 3/2 that of semi-full orbitals (those of covalence).

8.2.2 Methionine quantum structure

It turns out that Methionine, the amino acid initiator of all peptide chains working in living matter, has exactly double the number of entities as Glycine, previously studied.

Figure 20, the illustration of the detailed quantum structure of Methionine (in isolated molecular state) therefore reveals that number of true orbitals and that of stealthy orbitals are, as in glycined base, in a ratio of value 3/2. Again, in transcendence to this, another arithmetic phenomenon is revealed. It is also that the total number of stealth orbitals and filled orbitals is equal to 3/2 that of semi-full orbitals (those of covalence).

Unlike Glycine, Methionine has a larger atom: Sulphur. The detailed quantum configuration of this element (showing both true and stealth orbitals, see Figure 11) differs somewhat from C, N and O. However the overall arrangement of Methionine presents the same arithmetic arrangements opposing the different types of orbitals in 3/2 value ratios as in Glycine, the other fundamental amino acid used in the genetic code.

Fig. 20 Quantum structure of Methionine in a chevron form quantum chart: 60 orbitals whose 20 filled orbitals and 40 semi-full orbitals, 40 stealthy orbitals. 80 own electrons (in black)  and 40 guest electrons (in grey).See Fig. 7 and 8.

9. Synthesis of graphic and quantum proposals

Before the conclusion of this article, a synthesis of the proposals made as much on their graphic representation as on their existence is essential about true and furtive orbitals and the quantum shells where they evolve.

Figure 21 summarizes the proposals made in this paper about the graphical and quantum representations of electronic shells of chemical elements. Here are illustrated the first three shells, but of course the same representation remains valid beyond.

We therefore proposed the representation of these quantum shells in bi-dimensional spaces square shape and we intuitively filled empty proposing the existence of stealth orbits which can be also called "quantum gates." Finally, we propose that these quantum gates allow electrons to move instantly from orbitals to orbitals (and from atom to atom) by crossing singularities without space-time.

We have thus determined three possible quantum states in which these stealth orbitals can be found depending on the electronic environment that surrounds them but also generates them. Finally we were able to make several demonstrations of the functioning of all this electronic quantum structure in particular into the atomic and molecular components of the genetic code. The fact that arithmetic arrangements of the same nature are observed (in the form of a 3/2 ratio) as those previously introduced in the study [1] of the primordial constituents of the genetic code in the distribution of these real and stealthy orbitals reinforces the assumptions of existence of these last. 

Fig. 21 Electronic quantum chart depiction of chemical elements from classical linear quantum chart to detailed chevron form quantum chart then figurative chevron form quantum chart. See Fig. 1, 2, 15 and 16.

Conclusion

To illustrate the quantum composition of the various chemical elements, it is possible to represent, in a non-linear form, the distribution of the various electronic shells and subshells as well as the distribution of the orbitals which they contain.

It turns out that a graphic illustration of quantum shells representing them in the form of chevrons allows an instant viewing of the arithmetic connection operating between the number of these shells and the number of orbitals they can host.

In such representation, the groups of orbitals indeed appear in the form of a square structure whose size of the sides is directly proportional to the number of the shells, i.e. to the principal quantum number n.

Also, this new chart design is more explicit in describing the quantum structure of chemical elements and molecules they can form  than any other usual linear depiction.

For these reasons, we suggest that this graphics be privileged in the study and quantum descriptions of chemical elements (atoms) and molecules. Also, we propose the name of "chevron form quantum charts" to name this new physical graphic concept.

Intuitively, we think that this type of representation can reflect a true two-dimensional and quantum organization of the electronic clouds orbiting around atomic nuclei. Also, to fill the void of square-shaped quantum charts, we propose the existence of stealthy orbitals functioning as quantum gates and which allow the transit of electrons from orbitals to orbitals.

The fact that, in the components of the genetic code, orbitals and these quantum gates are in 3/2 arithmetic proportion reinforces our beliefs that the graphical quantum description of matter that is proposed in this article approaches physical reality.

References

1. Jean-Yves Boulay. Genetic code, quantum physics and the 3/2 ratio. 2020. ⟨hal-02902700⟩

Jean-Yves BOULAY independent researcher (without affiliation) – FRANCE -  e-mail: jean-yvesboulay@orange.fr

ORCID:0000-0001-5636-2375

From original paper here on ResearchGate: Chevron Form Quantum Charts

Full text in PDF: Chevron_form_quantum_charts

Règle du jeu

 La petite piste des nombres ultimes©

Ceci est la version courte du jeu La piste des nombres ultimes©

Description :   La petite piste des nombres ultimes© se joue de 2 à 4 joueurs sur un plateau numéroté de 0 à 50.

Matériel :         1 plateau numéroté de 0 à 50, 4 pions et 2 dés (numérotés de 1 à 6).

But du jeu :     Le but du jeu est d’atteindre le premier la case 50.

Déroulement :

Chaque joueur positionne son pion sur la première case (numérotée 0). Pour déterminer le premier joueur, chaque joueur lance un seul dé à tour de rôle.

Le joueur au plus haut score commencera la partie puis chaque autre joueur jouera à tour de rôle.

Le premier joueur lance alors deux dés et avance son pion d’autant de cases que la somme des deux dés. Si le joueur tombe sur un nombre ultime, il avance son pion sur le nombre ultime suivant. Si le joueur tombe sur un nombre élevé* (puissance d’un ultime) il recule son pion sur la case source* de ce nombre. Dans les autres cas, il reste en place. Le joueur suivant (placé à sa gauche si plus de 2 joueurs) joue à son tour et ainsi de suite.

Le gagnant est le joueur tombant le premier exactement sur la dernière case du jeu numérotée 50. Si le joueur fait un score dépassant cette case, il recule son pion de la différence à la case 50 (s’il arrive alors sur un nombre ultime, il recule son pion sur le précédent nombre ultime). Aux tours suivants, ce joueur, ayant passé par cette dernière case 50, pourra choisir de jouer avec deux dés ou un seul.

*Détail technique :

Un joueur tombant sur une des cases 4 – 8 – 16 – 32, doit repositionner son pion sur la case source 2 (par exemple 16 = 2 x 2 x 2 x 2)

Un joueur tombant sur une des cases 9 – 27, doit repositionner son pion sur la case 3.

Un joueur tombant sur la case 25, doit repositionner son pion sur la case 5.

Un joueur tombant sur la case 49, doit repositionner son pion sur la case 7.

La case 47 : si un joueur tombe directement sur la case 47, le dernier nombre ultime, il retourne alors sur la case 0 (la case de départ). S’il tombe sur la case 47 après avoir passé sur la case 50, donc en reculant, il positionne alors son pion sur la case 43, celle du nombre ultime précédent.

Plusieurs joueurs peuvent se trouver sur une même case.

La petite piste des nombre ultimes JY Boulay 2020 ©

Inspiré de : Jean-Yves Boulay. The ultimate numbers and the 3/2 ratio. 2020. ⟨hal-02508414v2⟩ 

→ un nombre ultime est un nombre qui n’a pas de diviseur plus petit que lui (autre que 1)

→ un nombre élevé est un nombre qui est une puissance d’un ultime et plus grand que cet ultime

Jeu inspiré de l'article : Les nombres ultimes et le ratio 3/2

 Télécharger le jeu à imprimer → La_petite_piste_des_nombres_ultimes

Ceci est la version courte du jeu La piste des nombres ultimes©

Au coeur du jeu !

Chaque joueur positionne son pion sur la première case (numérotée 0).

Le premier joueur lance alors deux dés et avance son pion d’autant de cases que la somme des deux dés.

 Si le joueur tombe sur un nombre ultime, il avance son pion sur le nombre ultime suivant. Si le joueur tombe sur un nombre élevé (puissance d’un ultime) il recule son pion sur la case source de ce nombre. Dans les autres cas, il reste en place. 

Le gagnant est le joueur tombant le premier exactement sur la dernière case du jeu numérotée 50.

Si le joueur fait un score dépassant cette case, il recule son pion de la différence à la case 50 (s’il arrive alors sur un nombre ultime, il recule son pion sur le précédent nombre ultime). 

Télécharger le jeu à imprimer →La_petite_piste_des_nombres_ultimes

Ceci est la version courte du jeu La piste des nombres ultimes©

Règle du jeu

 La piste des nombres ultimes©

Description : La piste des nombres ultimes© se joue de 2 à 4 joueurs sur un plateau numéroté de 0 à 99.

Matériel : 1 plateau numéroté de 0 à 99, 4 pions et 2 dés (numérotés de 1 à 6).

But du jeu : Le but du jeu est d’atteindre le premier la case 99.

Déroulement :

Chaque joueur positionne son pion sur la première case (numérotée 0). Pour déterminer le premier joueur, chaque joueur lance un seul dé à tour de rôle.

Le joueur au plus haut score commencera la partie puis chaque autre joueur jouera à tour de rôle.

Le premier joueur lance alors deux dés et avance son pion d’autant de cases que la somme des deux dés. Si le joueur tombe sur un nombre ultime, il avance son pion sur le nombre ultime suivant. Si le joueur tombe sur un nombre élevé* (puissance d’un ultime) il recule son pion sur la case source* de ce nombre. Dans les autres cas, il reste en place. Le joueur suivant (placé à sa gauche si plus de 2 joueurs) joue à son tour et ainsi de suite.

Le gagnant est le joueur tombant le premier exactement sur la dernière case du jeu numérotée 99. Si le joueur fait un score dépassant cette case, il recule son pion de la différence à la case 99 (s’il arrive alors sur un nombre ultime, il recule son pion sur le précédent nombre ultime). Aux tours suivants, ce joueur, ayant passé par cette dernière case 99, pourra choisir de jouer avec deux dés ou un seul. 

*Détail technique :

Un joueur tombant sur une des cases 4 – 8 – 16 – 32 – 64, doit repositionner son pion sur la case source 2 (par exemple 16 = 2 x 2 x 2 x 2)

Un joueur tombant sur une des cases 9 – 27 – 81, doit repositionner son pion sur la case 3.

Un joueur tombant sur la case 25, doit repositionner son pion sur la case 5.

Un joueur tombant sur la case 49, doit repositionner son pion sur la case 7.

La case 97 : si un joueur tombe directement sur la case 97, le dernier nombre ultime, il retourne alors sur la case 0 (la case de départ). S’il tombe sur la case 97 après avoir passé sur la case 99, donc en reculant, il positionne alors son pion sur la case 89, celle du nombre ultime précédent.

Plusieurs joueurs peuvent se trouver sur une même case.

La piste des nombre ultimes JY Boulay 2020 ©

Inspiré de : Jean-Yves Boulay. The ultimate numbers and the 3/2 ratio. 2020. ⟨hal-02508414v2⟩ 

→ un nombre ultime est un nombre qui n’a pas de diviseur plus petit que lui (autre que 1)

→ un nombre élevé est un nombre qui est une puissance d’un ultime et plus grand que cet ultime

Jeu inspiré de l'article : Les nombres ultimes et le ratio 3/2

 Télécharger le jeu à imprimer → La_piste_des_nombres_ultimes 

Ce jeu de plateau existe en version courte de 51 cases : La petite piste des nombres ultimes©

Au coeur du jeu !

Chaque joueur positionne son pion sur la première case (numérotée 0).

Le premier joueur lance alors deux dés et avance son pion d’autant de cases que la somme des deux dés.

 Si le joueur tombe sur un nombre ultime, il avance son pion sur le nombre ultime suivant. Si le joueur tombe sur un nombre élevé (puissance d’un ultime) il recule son pion sur la case source de ce nombre. Dans les autres cas, il reste en place. 

Le gagnant est le joueur tombant le premier exactement sur la dernière case du jeu numérotée 99.

Si le joueur fait un score dépassant cette case, il recule son pion de la différence à la case 99 (s’il arrive alors sur un nombre ultime, il recule son pion sur le précédent nombre ultime). 

 Télécharger le jeu à imprimer → La_piste_des_nombres_ultimes

Ceci est la version large du jeu La petite piste des nombres ultimes©

Un nombre ultime n'admet aucun diviseur non trivial lui étant inférieur

Genetic code, quantum physics and the 3/2 ratio

Quantum analysis of the atoms constituting the genetic code 

Jean-Yves Boulay

Abstract. The analysis of the quantum structure of the five chemical elements composing the coded twenty amino acids and the four coding nucleotides of DNA working in the organization of the genetic code reveals an opposition of their respective constituents in always an arithmetic ratio of value 3/2 according to the parity of the number of their quantum shells. Also, the quantum analysis of the amino acid Glycine, the smallest component of peptides that can be confused with saturated base, reveals the same arithmetic oppositions of 3/2 value of its components by the differentiation, operated according to their number of protons, of its five chemical groups. In sidelines to this study, a new graphic representation of the chemical elements is introduced: chevron form quantum chart.

From the original paper:Genetic_code_quantum_analysis

Genetic code, quantum physics and the 3/2 ratio

The analysis of the quantum structure of the five chemical elements composing the coded twenty amino acids and the four coding nucleotides of DNA working in the organization of the genetic code reveals an opposition of their respective constituents in always an arithmetic ratio of value 3/2 according to the parity of the number of their quantum shells.

https://hal.archives-ouvertes.fr

 Résumé

L’analyse de la structure quantique des cinq éléments chimiques composant les vingt acides aminés codés et les quatre nucléotides codant d’ADN oeuvrant dans l’organisation du code génétique révèle une opposition de leurs constituants respectifs en toujours un ratio arithmétique de valeur 3/2 selon la parité du nombre de leur couche quantiques. Aussi, l’analyse quantique de l’acide aminé Glycine, plus petit composant des peptides pouvant être confondu en base saturée, révèle les mêmes oppositions arithmétiques de valeur 3/2 de ses composants par la différenciation de ses cinq groupes chimiques opérée selon leur nombre de protons.

L'article complet en français : Code_Génétique_et_Physique_Quantique

1. Introduction

The genetic code is organized into two main entities including a coding structure, DNA (and/or RNA), made up of nucleotides and a coded structure, peptides, chains of amino acids. These two structures each consist of only five different atoms. Thus, Hydrogen, Nitrogen, Carbon, Oxygen and Phosphorus are the only elements of DNA (and RNA) the coding structure of the genetic code. All of the twenty amino acids that make up the peptides, the coded structure, are made up of Hydrogen, Nitrogen, Carbon, Oxygen and Sulphur. These two biological structures therefore each use three atoms with an even number of electron shells (C, N and O) versus two atoms with an odd number of quantum shells (H and P in DNA or H and S in amino acids). These two groups of chemical elements are opposed in various 3/2 value ratios according to almost all of their own quantum criteria.

2. Differentiation of atoms according to the parity of the number of electron shells.

Only five atoms make up the twenty genetically encoded amino acids. These five different atoms distribute their electrons over one, two and three quantum shells. According to these physico-chemical criteria, chart Figure 1, these five atoms are opposed in two groups in a duality of three versus two atoms: Carbon, Nitrogen and Oxygen are with even number of quantum shells; Hydrogen and Sulphur have an odd number of quantum shells. Still in a 3/2 ratio duality, the three atoms with an even number of electron shells total six shells (2 + 2 + 2 = 6 shells) versus four (1 + 3 = 4 shells) for the two atoms with odd number of quantum shells.

3. Quantum structure

By studying the quantum structure of these five atoms, a multitude of 3/2 ratios is revealed, opposing the three atoms with an even number of electronic shells to the two atoms with an odd number of electronic shells. DNA is also made up of the same five different qualities of atoms except that Phosphorus* replaces Sulphur. However, these last two atoms have the same number of electron shells and the same electronic structure in their saturated state (inside molecules) with the same maximum number of electrons that can orbit their nucleus. This means that the same 3/2 ratio dualities also operate in DNA.

* Phosphorus and Sulphur having the same saturated quantum configuration, these two elements can be confused in some demonstrations.

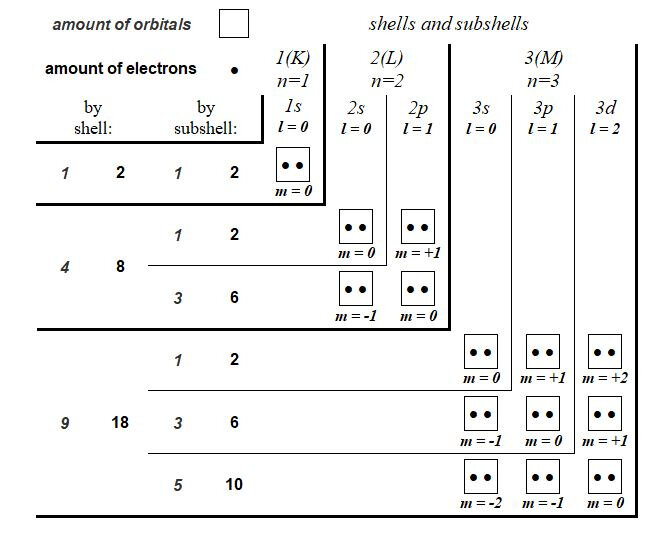
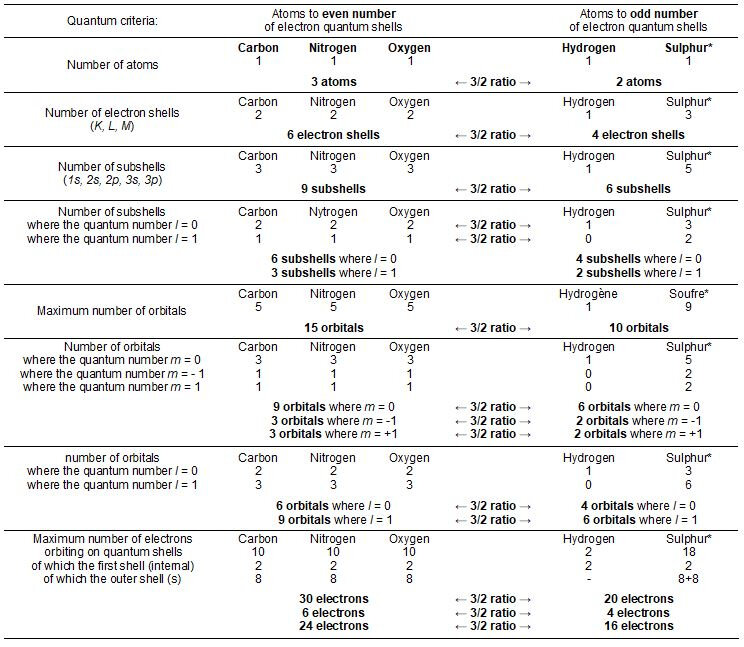
The chart in Figure 2 describes the quantum shells and subshells of electrons of the five atoms constituting the twenty amino acids as well as those of the Phosphorus for DNA. Also detailed are the values of the three quantum numbers n, l and m** as well as the numbers of orbitals. The description of the atoms is that in their saturated state, that is to say with their full electron shells such as they are inside amino acids or nucleotides (DNA).

** Here it is the quantum number m_ℓ which is the subject of study. For graphic simplification this value is simply noted m in the demonstrations.

The opposition of the values of Carbon, Nitrogen and Oxygen to those of Hydrogen and Sulphur (Phosphorus for nucleotides in DNA), always generates an arithmetic ratio of value 3/2 according to multiple criteria studied.

The table in Figure 3 lists the impressive series of quantum situations in which this remarkable duality takes place between sets of 3x entities versus 2x entities. Thus, the ratio for the numbers of electron subshells (1s, 2s, 2p, 3s, 3p) is 3/2. It is still 3/2 if we detail the subshells of those where the quantum number l = 0 of those where the quantum number l = 1.

Also, the ratio for the numbers of orbitals is 3/2. It is still on 3/2 if we detail the orbitals of those where the quantum number m = 0, of those where the quantum number m = - 1 and those where the quantum number m = 1. This ratio is always 3/2 if we detail the orbitals of those where the quantum number l = 0 of those where the quantum number l = 1. Also, the maximum number of electrons that can orbit inside all of the electronic shells of these two groups of atoms is still in a ratio of 3/2: thirty electrons can orbit inside the electronic shells of Carbon, Nitrogen and Oxygen versus twenty on the electron shells of Hydrogen and Sulphur (Phosphorus for DNA bases).

For this last criterion, the distinction of the electrons which can orbit either on the first internal shell (2 electrons for each of the five atoms) or on the set of the other (external) shells always opposes the different values in ratios 3/2: 6 versus 4 electrons for the inner shell and 24 versus 16 for the other shells.

Thus, fourteen different quantum criteria oppose, in a duality of ratio 3/2, the five atoms constituting the twenty amino acids (and also constituting the four DNA bases with the Phosphorus in place of Sulphur). The fact that the genetic code is organized only with these five different atoms in this duality is therefore not random. The perfect complementarity of the quantum characteristics of Hydrogen and Sulphur (Phosphorus in DNA) is particularly remarkable. These last two atoms have indeed very different quantum characteristics (in contrast to Carbon, Nitrogen and Oxygen with common characteristics) which however complement each other perfectly to always oppose in a 3/2 ratio to three other atoms, constituents of amino acids (and DNA bases). For example, Sulphur has a maximum number of nine orbitals versus only one for Hydrogen. These two very different values nevertheless complement each other (10 orbitals) to oppose in a duality of ratio 3/2 to the three times five quantum orbitals of Carbon, Nitrogen and Oxygen (15 orbitals).

Thus, the 3/2 ratio is revealed at the bottomest of the subatomic structure of the constituents of the twenty amino acids that are on the one hand the three atoms of Carbon, Nitrogen and Oxygen and on the other hand the two atoms of Hydrogen and Sulphur. It is therefore remarkable to note that these same phenomena are found in DNA, another mechanical component of the genetic code, where the quantum properties of the Phosphorus mimic those of Sulphur.

Also, Figure 4, these six atoms constituting the entire mechanism of the genetic code therefore oppose three to three depending on the parity of their number of electron shells. In a ratio of 3/2, the Hydrogen - Phosphorus - Sulphur group totals 63 (3 times 21) nucleons versus 42 (2 times 21) for the Carbon - Nitrogen - Oxygen group. These same two groups are inversely opposed in the 3/2 ratio with respectively nine valences for C, N and O versus six valences for H, P and S.

4  Quantum analysis

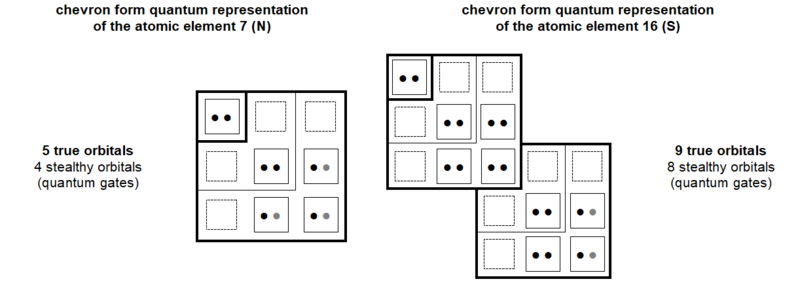
4.1 New quantum chart

This quantum study of the genetic code is an opportunity to propose a new type of table describing the quantum organization of atoms. In this chart, illustrated in Figure 5, the different quantum shells and subshells are presented in the form of chevrons. At the top end of each rafter are indicated the names of the different shells and subsells; at the left end of these chevrons, the numbers of orbitals and electrons of these different shells and quantum subshells are indicated. At each chevron vertex is the orbital where the quantum number m = 0. The orbitals with positive quantum number m are progressively positioned towards the top of these chevron vertices and the orbitals with negative quantum number m are progressively positioned towards the outside left of these chevron vertices.

In the appendix, the same type of table is presented describing the quantum organization of the shells and subshells up to the 5th shell (O) and 15th subshell (5g). This innovative presentation, more explicit in describing the quantum structure of the atomic elements, will be used in various tables of this quantum study of the constituents of the genetic code.

 4.2 Quantum structure of atoms

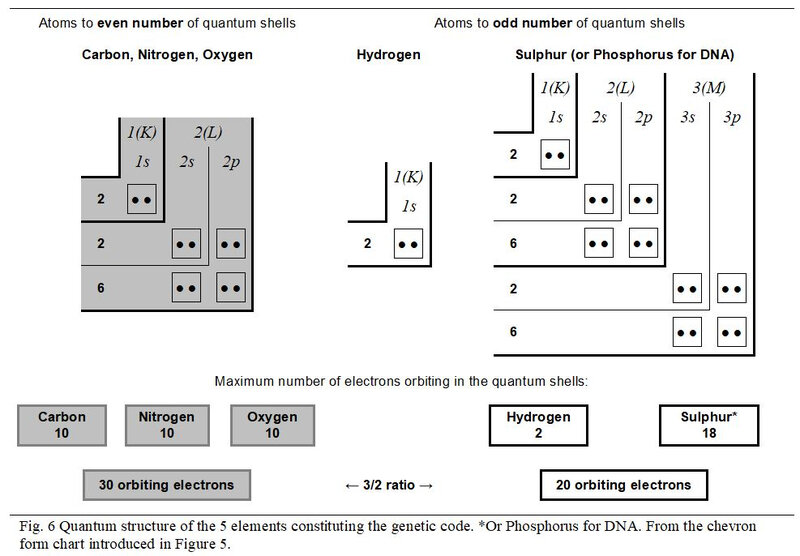
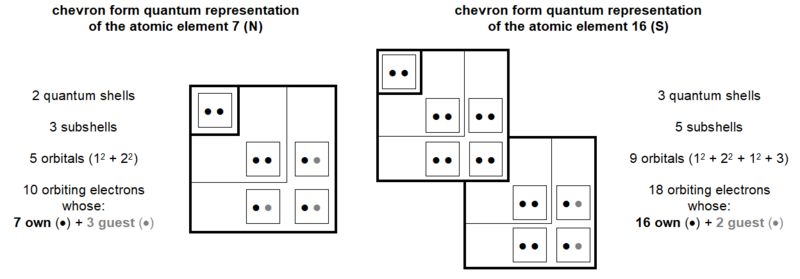
Figure 6 illustrates the quantum structure of the five atoms working in the genetic code. As stated above, the Phosphorus, working in DNA and the Sulphur, involved in peptides, are confused in this analysis. Also, the three atoms Carbon, Nitrogen and Oxygen with even number of quantum shells present the same quantum configuration in their saturated state.

As already introduced in Figure 3, it appears more explicitly in this type of chevron form chart that, in a 3/2 value ratio, the 30 electrons (10 + 10 + 10) orbiting in the three atoms with an even number of quantum shells oppose the 20 electrons (2 + 18) orbiting in the two chemical elements with an odd number of quantum shells.

4.3 Azimuthal quantum number

Figure 7 details the distribution of electrons according to the value of the azimuthal quantum number. It appears that according to this criterion and the parity of the number of quantum shells, the distribution of the electrons of these three and two elements is organized into numerous ratios of 3/2 value including ratios transcendent according to the criteria considered. This arithmetic transcendence is directly related to the remarkable identity (a + b)² = a² + 2ab + b² where a and b have the respective values 3 and 2. This relationship to the remarkable identity which operates in several of the next tables is illustrated and explained in Chapter 4.7.

4.5 Magnetic quantum number

Illustrated in figure 8, the distinction between electrons with a magnetic number m = 0 and those with a magnetic number m = -1 or m = +1 generates exactly the same transcendent arithmetic ratios of 3/2 value. It is essential to emphasize that despite different individual values for the elements H and S, the same global values are found in these counts from two different quantum criteria: the azimuthal quantum number (l) and the magnetic number (m).

4.6 Quantum shells

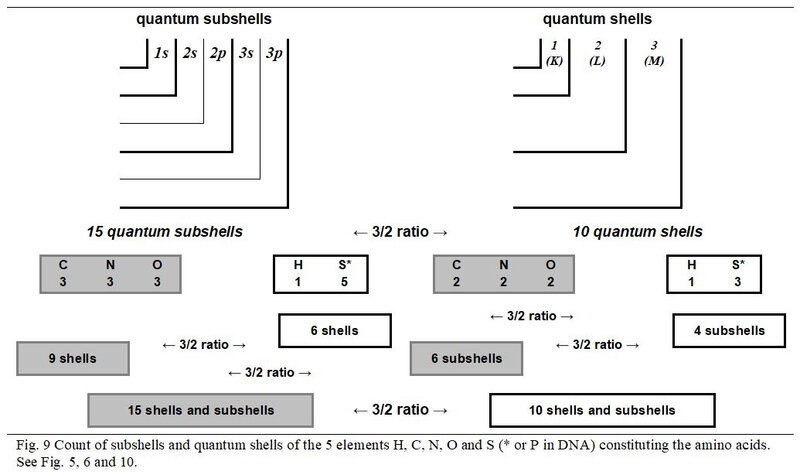
As illustrated in Figure. 9, the individual number of subshells of the three chemical elements C, N and O (with even number of shells) is equal to 3/2 of their number of quantum shells. The values of these same ratios are to 1/1 for Hydrogen and 5/3 to Sulphur. However, the global values of these two elements with an odd number of shells complement each other perfectly to also generate a 3/2 ratio between their number of subshells and shells but also with the global values of the three atoms with an even number of quantum shells.

4.7 Remarkable identity

Thus, these various ratios opposing the subshells and shells and transversely, the two categories of atoms previously defined according to the parity of their number of quantum shells, are organized in the remarkable identity (a + b)² = a² + 2ab + b² where a and b have the respective values 3 and 2. Figure 10 explains this arithmetic organization operating in the quantum structure of the five elements working within the genetic code.

Thus, the quantity of subshells in C, N and O corresponds to the value a² of the remarkable identity and the quantity of subshells in H and S corresponds to the value ab. The quantity of quantum shells in C, N and O also corresponds to the value ab and that in H and S corresponds to the value b². These different values therefore transcend into these equal ratios:

(a²/ab) = (ab/b²) = (a²+ab)/(ab+b²) 

(3²/6) = (6/2²) = (3²+6)/(6+2²) 

(9/6) = (6/4) = (15)/(10)

As it was previously revealed, this remarkable identity therefore also operates in the counts of electrons according to their azimuthal quantum number (Figure 8) and according to their magnetic number (Figure 9). In these electron counts, the values are just double and, for a and b at the root values 3 and 2, the respective and transcendent values are equal to:

2a²→ 2ab → 2ab → 2b²

18 → 12 → 12 → 8

 5 Anatomy of Glycine

Within the mechanism of the genetic code and therefore among the twenty amino acids, Glycine is distinguished by its absence of radical. Its radical is reduced to a simple hydrogen atom which in a way simply closes the "base" structure common to each amino acid. The quantum study of this glycined base, identifying with Glycine, reveals singular arithmetic arrangements of its different components.

5.1 Modules of Petoukhov

The notion of modules is an original system proposed by Sergei Petoukhov [1;2] to describe the structure of biological molecules. In the appendix is introduced this concept of modular structure and detailed two sets of amino acids with the number of protons equal or not equal to eight times their respective number of Petoukhov modules.

5.2 Detailed structure of Glycine

Figure 11 describes the structure of Glycine (or saturated base called glycined base) according to many criteria including its chemical composition, modular, but also atomic. It turns out that Glycine consists of 40 protons, either 5x protons or (3 + 2)x protons. This glycined base also consists of 5 groups or modules, i.e. (3 + 2)x chemical groups. In Glycine, the number of protons is therefore an exact multiple of 8 (5 times 8 protons) and it turns out that the average number of protons per chemical group (or Petoukhov module) is therefore 8. For two groups ( CH₂ and O), the amount of protons is exactly 8 whereas for the other three groups, these proton amounts are 9 or 6 (NH₂ → 9, OH → 9 and C → 6).

The differentiation of these two types of modules, made up or not made up of 8 protons reveals a multitude of oppositions of the different natures of the components of Glycine (glycined base) in always an arithmetical ratio of 3/2 value. As described in the appendix, the multiplicity of protons/modules within an 8/1 ratio of amino acids is not random, but concerns exactly 50% of the twenty amino acids used in the genetic code, i.e. 10 amino acids out of 20.

Glycine is made up of a multitude of entities whose numbers are all multiples of five. Thus the glycined base consists of five modules, two times five atoms, five of which have one electron shell (H) and five at two shells (C, N and O). Also Glycine consists of 5 times 15 nucleons (75) including 5 times 7 (35) neutrons and 5 times 8 (40) protons. The covalent bonds between these different components are also in numbers which are multiple of 5.

Also, it therefore appears, Figures 11 and 12, that the different constituents of Glycine, always 5x in number, are always at 3 same x entities in the set of three modules (chemical groups) with number of protons not equal to 8 and always of amount at 2 same x entities in the set of two modules whose number of protons is equal to 8.

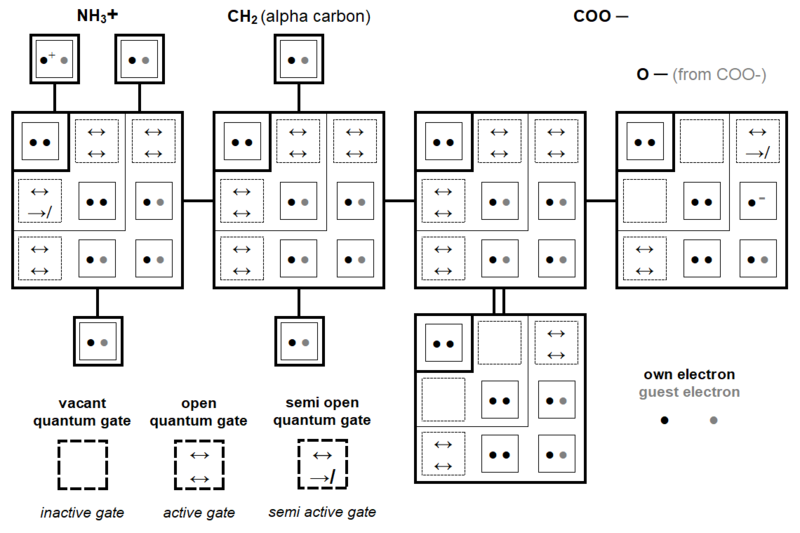
5.3 Quantum analysis of the glycined base

In the next Figures 13 and 17, the detailed quantum structure of Glycine (shown as glycined base) is illustrated. This graphic representation, more explicit than a classic version, is inspired by the concept of chart in chevron introduced in Chapter 4.

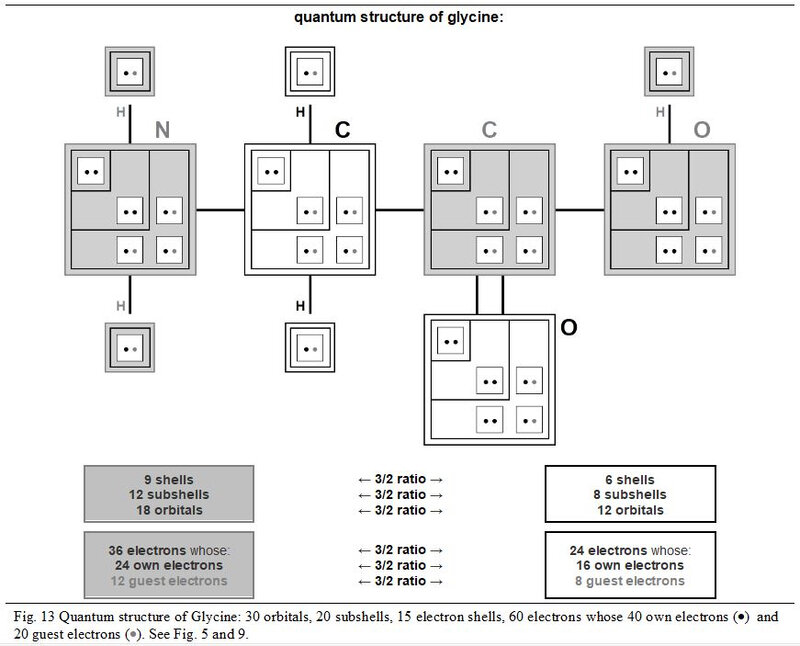
In its quantum structure, Glycine (glycined base) is therefore also always made up of 5x entities. Its ten atoms total 15 (5x → x = 3) quantum shells and 20 (5x → x = 4) electron subshells. These 20 subshells total 30 (5x → x = 6) orbitals where 60 (5x → x = 12) electrons can evolve, including 40 (5x → x = 8) individually own to these ten atoms and 20 (5x → x = 4) covalent electrons (20 shared electrons).

5.3.1 Orbitals, shells, and quantum subshells

Depending on whether they are in the three modules with a number of protons not equal to 8 or in the two with a number of protons equal to 8, these various entities are always with the respective numbers of 3x and 2x. Thus, in these two groups of modules we can oppose, in a ratio of 3/2, 18 orbitals to 12 others, 9 quantum shells to 6 others and 12 subshells to 8 other subshells.

Also, as illustrated in Figure 14, the values of the orbitals and of the quantum subshells oppose in transcendent ratios of value 3/2. So more, this arithmetic transcendence is organized from the remarkable identity (a + b)² = a² + 2ab + b² where a and b have the respective values 3 and 2.

In these counts, the respective and transcendent values are equal to two times the root values of this identity, that is:

2a²→ 2ab → 2ab → 2b²

18 → 12 → 12 → 8

5.3.2 Orbiting electrons and own electrons

As illustrated in Figure 15, depending on whether they are specific to each atom or orbiting (own + invited), and according to their membership of one or the other type of modules (chemical groups previously defined), the electrons of Glycine s oppose in transcendent ratios on 3/2 value. Also, this arithmetic transcendence is organized from the remarkable (a + b)² = a² + 2ab + b² where a and b are to respective values 3 and 2.

In these counts, the respective and transcendent values are equal to four times the root values of this identity, that is:

4a²→ 4ab → 4ab → 4b²

36 → 24 → 24 → 16

5.3.2.1 Electric charges and 3/2 ratio

Since the numbers of clean electrons correspond to those of the numbers of protons, the negative and positive electric charges are therefore also opposed in a ratio of value 3/2 with, for the whole of Glycine, 60 electrons (orbiting) charge negative (-e) versus 40 protons of positive charge (e). The same opposition of electric charges is observed in the two groups of modules previously defined with, for one and the other group, 36 negative charges versus 24 positive and 24 negative charges versus 16 positive charges.

5.3.3 Own electrons and electron sharing

In Glycine, the number of semi-full orbitals is double the number of full orbitals. Also, as illustrated in Figure 16, the distribution of these two types of orbital is organized in 3/2 value ratios between the two groups of modules previously defined according to their proton number equal or not equal to 8.

5.3.4 Jumps in quantum shells

Figure 17 describes, for each atom of Glycine, the amplitude of subshell jumps of electrons which are shared with another atom. Among the 20 shared electrons, it turns out that 10 change (jump) subshell level and 10 do not change level (see also Figure 20).

For example (Figure 18), in the NH₂ group (module), the own electron of the Hydrogen atom evolves on its original level 1 subshell and on the level 3 subshell of the Nitrogen atom.

5.3.4.1 Jumps and levels of quantum subshells

As it appears Figures 17 and 19, the counting of these subshell jumps always registers in a ratio of 3/2 according to the membership of the electrons to one or the other of the two groups of modules (chemical groups) differentiated according to their number of protons. Also, for each of the shared electrons, the distribution of the cumulative levels of the subshells where these electrons orbit are still organized in a 3/2 value ratio according to these same criteria of differentiation of the modules considered.

5.3.4.2 Electrons shared and subshells

As shown in Figure 20 and previously Figure 17, in their covalent migration, 50% of the shared electrons change of subshell level and 50% are found on the same quantum level. The count of these two types of migration in one and the other group of modules previously defined according to their number of protons is written in arithmetic ratios of value 3/2 with, for each type of migration, six electrons versus four.

5.4 Bonds (valences) and modules

According to the concept of modular structure proposed by Sergei Petoukhov, concept introduced in Chapter 5.1 and detailed in the appendix, it is possible to differentiate two types of covalent bonds:

- the module↔module bonds operating between two non-hydrogen atoms,

bonds which can be qualified as master–master,

- the module↔Hydrogen bonds operating between a Hydrogen and a non-hydrogen atom,

bonds which can be qualified as master–satellite.

As demonstrated in Figure 21 and more explicitly in Figures 13 and 17 where the modular and quantum structures of the atoms are illustrated, the cumulative numbers of master-master bonds and of master-satellite bonds are identical in Glycine (glycined base), i.e. ten bonds (cumulated per atom) for these two categories of covalent bonds.

Also, the distribution of these two types of bonds is organized into 3/2 value ratios between the two groups of modules previously differentiated according to their number of protons which can be equal or not equal to 8.

 5.5 Radius and electronegativity

The study of the different main physical values of the chemical elements constituting Glycine* and listed in the table in Figure 22 reveals some like arithmetic phenomena opposing the three modules with a number of protons not equal to 8 to the two with number of protons equal to 8. 

5.5.1 Atomic radii

As illustrated in Figure 23, the cumulation of the individual values of the covalent radii, the atomic radii and the Van der Waals radii of the chemical elements constituting the Glycine also register in arithmetic ratios of 3/2 value by the opposition of the two groups of modules previously defined according to their number of protons.

These ratios are not all exactly equal to the 3/2 arithmetic value but approach more than 99%. These differences are justified by the lack of precision (rounding of values) of the source data.

*Note: the values considered are those of the elements in their primordial state.

5.5.2 Electronegativity

As illustrated in Figure 24, the cumulative individual values of the electronegativity of the chemical elements constituting Glycine also fall into arithmetic ratios of 3/2 by the opposition of the two groups of modules previously defined according to their number of protons. This is true from the Allred scale, from the Pauling scale and also from the Mulliken scale with slight oscillations of the ideal ratio of 3/2.

Again, these ratios approach at more than 99% of the ideal 3/2 value ratio and these differences are justified by the variability and relative imprecision of the raw source data on these different scales.

Thus, although different individually, these different physical values of atomic dimension and electronegativity are nevertheless and always organized in arithmetic ratios of value 3/2 by the opposition of the modules (chemical groups) with equal or unequal proton number to the value 8.

6 Quantum analysis of Methionine

We have just demonstrated that the quantum study of Glycine reveals an organization of its components in various arithmetic arrangements, mainly the 3/2 ratio. With less amplitude, but still very significantly, another proteinogenic amino acid, quantically organizes itself in similar arrangements. This amino acid is not just any, it is Methionine, initiating (and being the only one in this case) any peptide chain.

Figure 25 describes the quantum structure of Methionine where a maximum of 120 electrons can orbit, a value double that of Glycine and also equal to 5x. 

Fig. 25 Quantum structure of proteinogenic amino acid Methionine. See Fig. 26 and 27 also.

6.1 All orbiting electrons versus own electrons

In the next Figures 26 and 27 is counting some quantum values of Methionine: orbiting and own electrons, orbitals and subshells.

Exactly like for Glycine (See Figure 15, Chapter 5.3.2), as illustrated Figure 26, the quantity of electrons that can evolve on the orbitals of Methionine (120 electrons) and the quantity of electrons which are own to this amino acid (80 electrons) are opposed in a ratio of value 3/2.

6.2 Orbital amount versus subshell amount

Exactly like for Glycine (See Figure 14, Chapter 5.3.1), as illustrated Figure 27, the quantity of atomic orbitals of Methionine (60 orbitals) and the quantity of subshells inside atoms of this amino acid (40 subshells) are opposed in a ratio of value 3/2.

7 Quantum configuration of carbon

Among the five chemical elements constituting proteinogenic amino acids and more broadly within the various organic molecules, it is recognized that carbon plays a primordial role. The following observation is therefore not timely.

7.1 Carbon and 3/2 ratio

As illustrated in Figure 28, since its excited state then becoming saturated, carbon can therefore total ten electrons on its orbitals, including six own electrons and four guest. These two sets of electrons are thus opposed in a 3/2 value ratio. Of the five chemical elements that make up amino acids (H C N O S, see Figures 2 and 13) or DNA/RNA (H C N O P), only Carbon has this 3/2 ratio between own and guest electrons.

8 The first ten chemical elements

From the viewpoint of filling the orbitals, the first ten chemical elements deserves special development. Thus, Figure 29, the chemical element of number 10, is the one which completely fills the first three quantum subshells.

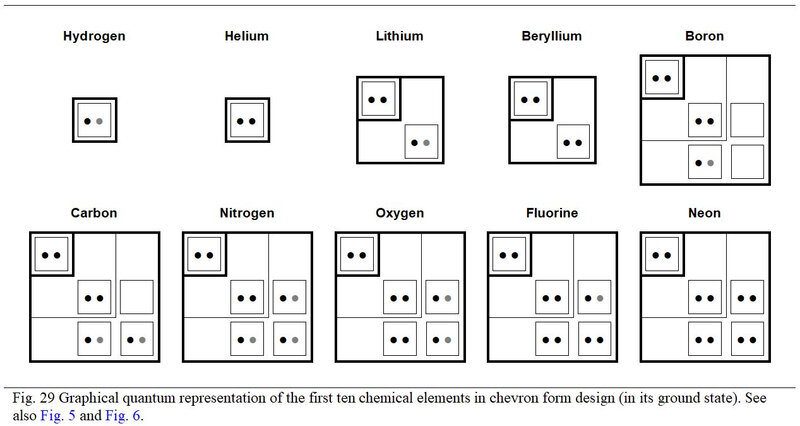
Also, the own values of the atomic numbers of these first ten elements generate singular arithmetic phenomena to whether these elements are inorganic or organic. Moreover, for these first ten chemical elements, the distribution in detail of their electrons according to the parity of the rank of the quantum subshells is particular. It is necessary to highlight this before concluding this quantum study of the genetic code.

8.1 Inorganic versus organic elements

It turns out that among the first ten chemical elements, in a 3/2 ratio opposition, six are not used in the genetic code (Helium, Lithium, Beryllium, Boron, Fluorine and Neon) while four elements (Hydrogen, Carbon, Nitrogen and Oxygen) are used. More generally, we can therefore say that six of these ten chemical elements versus four are not elements of living matter since they do not compose organic molecules.

Also, as it appears in Figure 30, the sums of the own electrons of these two groups of six and four chemical elements are as well opposed in an arithmetic ratio of value 3/2. It turns out that the group of six inorganic elements totals 33 electrons while that of the four organic elements totals 22.

8.2 Odd subshells versus even subshells

Top Figure 31 shows that in a ratio of 3/2 value, the first 6 inorganic chemical elements total 24 electrons into their odd subshells (1s and 2p)  versus 16 electrons for the first 4 organic chemical elements.

Down Figure 31 shows that in a ratio of 3/2 value, the first 6 inorganic chemical elements total 9 electrons into their even subshells (2s)  versus 6 electrons for the first 4 organic chemical elements.

All this is observed by considering these elements in their ground state as described in Figure 29.

 Discussion et  Conclusion

Analysis of the quantum organization of the chemical elements working in the constituents of the genetic code reveals a systematic opposition of their different components in a 3/2 value ratio depending on whether these atoms have an even or odd number of quantum shells. The multitude of these singular arithmetic arrangements, always identical in their final ratios, prohibits the idea of any random interaction of these different constituents.

These arithmetic configurations are of a highly structured level, often even organized around the remarkable identity (a + b)² = a² + 2ab + b² where a and b have precisely the respective values 3 and 2. The arithmetic mechanics arising of this identity thus allows the different values considered to be organized and opposed in a triple ratio of 3/2 transcendent values and in arithmetic form: (a²/ab) = (ab/b²) = (a²+ab)/(ab+b²).

In another paper [3] and yet in a very different scientific field, that of the study of whole numbers, we also observed the organization of entities in this 3/2 ratio and also in this same remarkable identity. This therefore supports the idea of a universality of these arithmetic phenomena.

As highlighted in some of his various works including those referenced in [1] and [2], Sergei Petoukhov draws attention to the organization of the components of the genetic code around the values 3 and 2. For example , and this is of great importance, there are two types of DNA base associations, one with three hydrogen bonds between the bases Guanine and Cytosine and the other with two hydrogen bonds between the bases Adenine and Thymine.

The fact that this 3/2 arithmetic ratio also operates between the components of Glycine, the primary amino acid identified to a glycined base, supports the idea of an arithmetically non-random organization of the mechanics of the genetic code. The latest investigations studying the different values of radii and electronegativity of the components of this glycined base greatly reinforce this analysis.

In this organization of living matter, its modular structure, the multiplicity (or not multiplicity) protons/modules and more broadly the multiplicity (or not multiplicity) of the numbers of protons of the twenty amino acids by the value 8 appear to be factors to consider with the utmost care. Also, we suggest, without discussing it further here, that this criterion of multiplicity by 8 of the number of protons in amino acids is related to the byte rule, another quantum constraint operating in the chemical elements used in these amino acids.

To conclude this quantum study of the components of living matter working in the organization of the genetic code, we advance the idea that this matter known as "living" is only the prolongation of a general organization of matter since its atomic structure towards its molecular structure. Indeed, as it is revealed in this study, the elements working within living matter are not randomly organized  according to arithmetic criteria which depend on their primordial quantum structure.

This 3/2 fractional value arithmetic ratio is very similar to the fractional values of the electric charges of different quarks, which are ratios of whole numbers (2/3 and -1/3). Thus these phenomena, operating in the most complex organization of matter, depend on its most basic structure. By the amplitude of the phenomena presented here, it is therefore not possible to imagine a non-relation between this primary structure of matter and its highly organized structure as it appears in the structural mechanics of the genetic code.

Appendix

A1. Quantum chart in chevron form

A1.1 New quantum chart

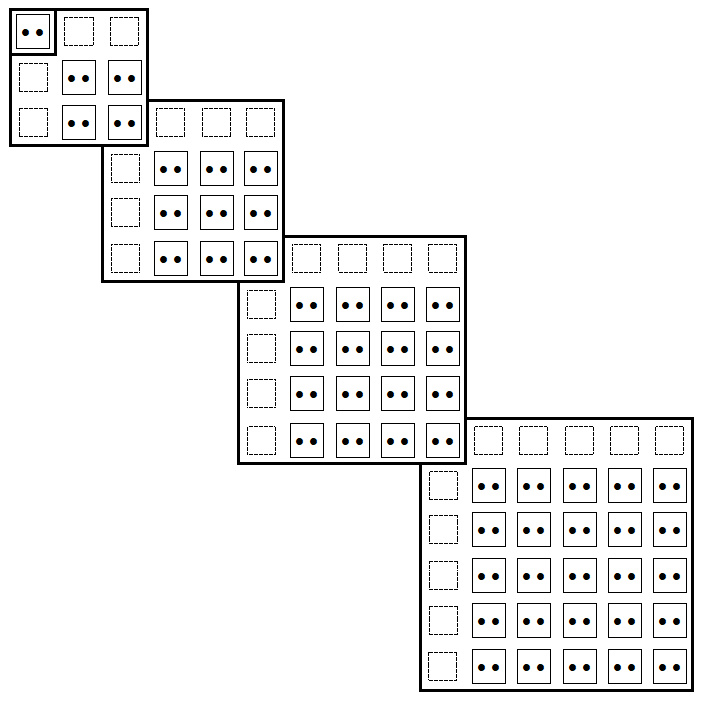
Figure 32 shows the new chevron form quantum table of the first 15 electronic shells. This graphic concept is introduced in Chapter 4.1 and illustrated in Figure 5. We suggest that this new graphic type be favoured for the description of the quantum organization of the different chemical elements.

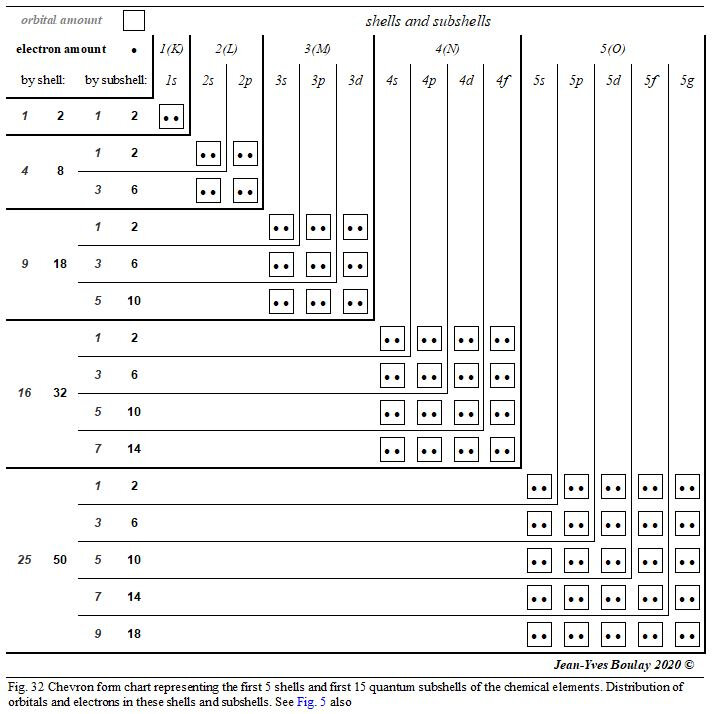
A1.2 Quantum chart depiction

In this table, the different quantum shells and subshells are presented in the form of chevrons. At the top end of each rafter are indicated the names of the different shells and subshells; at the left end of these chevrons, the numbers of orbits and electrons of these different shells and quantum subshells are indicated. At each chevron vertex is the orbital where the quantum number m = 0. The orbitals with positive quantum number m are progressively positioned towards the top of these chevron vertices and the orbitals with negative quantum number m are progressively positioned towards the outside left of these chevron vertices.

This new graphic design is more explicit in describing the quantum structure of atomic elements than any other usual linear chart. Very visually, this chevron configuration clearly highlights the arithmetic progression of the orbital numbers of the different quantum shells in square powers of the level of these electronic shells: 

- 1^st shell →           1² = 1 orbital,

- 2^nd shell →          2² = 4 orbitals,

- 3^rd shell →          3² = 9 orbitals,

- 4^th shell →          4² = 16 orbitals, etc.

A.1.3 Atom quantum chart

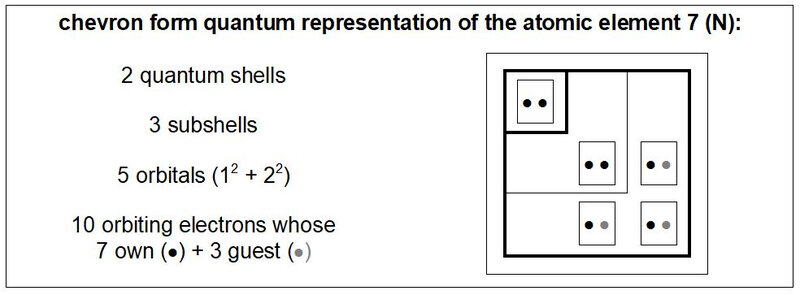
 In this table, and more generally in this quantum study of the chemical elements, constituents of the genetic code, the electronic spin is not detailed (by ascending or descending arrows). In return, it is the migratory or non-migratory nature of the electrons that is about development. Thus, for example, the representation of the nitrogen atom such as that illustrated in Figure 33 (and in various other figures of this quantum study) is favoured.

A.2 Number of protons and modules of the twenty amino acids

A.2.1 Modules of Petoukhov

The notion of module is an original system proposed by Sergei Petoukhov [1 and 2] to describe the structure of biological molecules. This system represents each non-hydrogen atom by the number of protons in its nucleus. For example, the nitrogen atom is represented by the number 7. If one or more hydrogen atoms are joined to a non-hydrogen atom, the number of hydrogen protons is added to the number of atom protons of non-hydrogen.

Thus, such a group made up of a non-hydrogen atom and its adjoining satellite atoms of Hydrogen is defined by the total sum of protons of this group and this set is called "module". Figure 34 illustrates this modular concept applied to amino acids.

For example, the amide group NH₂ forms a module: it is denoted by the number 9 which is the sum of 7 protons of one nitrogen atom and 2 protons of two satellite atoms of Hydrogen. Sergei Petoukhov provides [1 and 2] modules from 6 to 9 protons according to the configurations. Thus according to this system, the Sulphur atoms (present in Met and Cys) break down conventionally into two modules of 8 protons (or 9 protons if associated with a Hydrogen in Cys).

A.2.2 Protons/modules multiplicity

The genetic code is organized only with 20 amino acids. Figure 35 isolates amino acids with a number of protons multiple of the number of modules from those with a number of protons not multiple of the number of modules. It turns out that these two groups are of equal size since they each consist of 10 entities.

It is remarkable to note that the respective number of protons of each of the ten amino acids of the first group, that whose number of protons is multiple of the number of modules, is always equal to eight times the number of modules.

Also, for this first group of ten amino acids, the total number of modules is equal to 80, so an average of 8 modules into each amino acid. Thus, the total number of protons in this group is therefore equal to 640 protons, an average of 64 (8²) protons by amino acid. Also, for each of the ten other amino acids, the proton/module ratio never represents an integer but a fraction different from x/1 (x being an integer).

A.2.3 Other multiplicities

The number of proteinogenic amino acids is 20 and this number is not by chance. It is equal to 5x (5x → x = 4). This value therefore allows the formation of a 3/2 ratio since this number is therefore equal to 3x + 2x (3x + 2x → x = 4).

As described in the left part of Figure 36, it turns out that two other amino acids have a number of protons multiple of 8 but not multiple of their respective number of modules: Phe with 88 protons for 12 modules and Tyr with 96 protons for 13 modules. Thus, by these multiplicity criteria, in a ratio of value 3/2 are opposed twelve amino acids with number of protons multiple of 8 versus eight amino acids with number of protons not multiple of 8.

Also, as described in the right part of Figure 36, in an inverse ratio of 2/3 value, height amino acids versus twelve have a number of protons multiple of their respective number of chemical groups. As explained above, the nuance between chemical groups and modules is observed for chemical groups composed of a sulphur atom, an atom conventionally made up of two modules (see Figure 27). Thus, the amino acids Cys and Met have an amount of chemical groups which differs to one value in relation to their number of modules.

A.2.4 Three progressive arithmetical ratios

Thus, illustrated in Figure 37, according to three different criteria for the multiplicity of proton numbers, the ratio between the twenty amino acids operating in the genetic code changes from the value 3/2 to the value 1/1 then to the value of 3/2 , inverse to the initial.

All these observations confirm the differentiations made in the chemical, quantum and atomic study of Glycine between the modules (chemical groups) with a proton number equal to 8 and from the modules with a proton number not equal to 8.

References

1. S.V.Petoukhov. Genetic Code and the Ancient Chinese Book of Changes, Symmetry Culture and Science, vol.10. 1999.

2. S.V.Petoukhov. The Bi-periodic Table of Genetic Code and Number of Protons. 2001.

3. Jean-Yves Boulay. The ultimate numbers and the 3/2 ratio. 2020. ⟨hal-02508414v2⟩

4. www.elementschimiques.fr

Jean-Yves BOULAY independent researcher (without affiliation) – FRANCE -

e-mail: jean-yvesboulay@orange.fr

https://orcid.org/0000-0001-5636-2375

Original full text here:Genetic_code_quantum_analysis

L'article complet en Version française :Code_Génétique_et_Physique_Quantique

Jean-Yves BOULAY

The universal 3/2 ratio

 Jean-Yves Boulay

 The 3/2 ratio appears in three studies from different fields. This universal operates in the initial organization of integers, in the order of the first appearance of the 10 digits in many mathematical constants and in the quantum structure of the 5 constituent elements of proteinogenic amino acids.

Here is just an overview of these three studies of this universal ratio.

 3/2 ratio and whole numbers:

From the first ten numbers of the three source classes of whole numbers, generation inside 3/2 ratios of the first ten numbers of each of the four final number classes: the 40 primordials:

From the paper: Jean-Yves Boulay. The ultimate numbers and the 3/2 ratio. 2020. ⟨hal-02508414v2⟩

https://hal.archives-ouvertes.fr/hal-02508414v2

https://www.researchgate.net/publication/339943634_The_ultimate_numbers_and_the_32_ratio

10.13140/RG.2.2.32843.34081/2

3/2 ratio and decimals of mathematical constants:

 The sum of the ten figures of the decimal system, considered as numbers in this paper, is 45:

0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45

This number is sum of two others: 45 = 27 + 18. These two numbers have a ratio to 3/2 and are respectively equal for 3 times and twice 9. The number 10, which here represents the ten possible occurrence ranks of the ten figures of the decimal system, has the same characteristics: sum of two other one numbers with a ratio to 3/2: 10 = 6 + 4.

There appears that for Pi, 1/Pi and Phi (φ) the ten digits of the decimal system are organized in a ratio to 3/2: the sum of first six digits is to 27 and the last four to 18. This phenomenon of ratio to 3/2 (27/18) is present in other significant constants. This arithmetical phenomenon is not therefore haphazard. This phenomenon is present in constants as ζ (5) (Zeta 5 function), number e (constant of Neper), in constants of Copeland and Kaprekar. Also, in significant fractions relating directly to the decimal system as the fraction 9876543210/0123456789.

From the paper: Pi and Golden Number: not random occurrences of the ten digits

https://www.researchgate.net/publication/336035070_Pi_and_Golden_Number_not_random_occurrences_of_the_ten_digits

3/2 ratio, genetic code and quantum physics:

Only five atoms make up the twenty genetically encoded amino acids. These five different atoms distribute their electrons over one, two and three quantum shells. According to these physico-chemical criteria, these five atoms are opposed in two groups in a duality of three versus two atoms: Carbon, Nitrogen and Oxygen are with even number of quantum shells; Hydrogen and Sulphur have an odd number of quantum shells. Still in a 3/2 ratio duality, the three atoms with an even number of electron shells total six shells (2 + 2 + 2 = 6 shells) versus four (1 + 3 = 4 shells) for the two atoms with odd number of quantum shells. The opposition of the values of Carbon, Nitrogen and Oxygen to those of Hydrogen and Sulphur (Phosphorus for nucleotides in DNA), always generates an arithmetic ratio of value 3/2 according to multiple criteria studied.

From the paper: Jean-Yves Boulay. Genetic code, quantum physics and the 3/2 ratio. 2020. ⟨hal-02902700⟩

https://hal.archives-ouvertes.fr/hal-02902700

https://www.researchgate.net/publication/343064455_Genetic_code_quantum_physics_and_the_32_ratio

10.13140/RG.2.2.26505.67681/3

 The universal 3/2 ratio

Jean-Yves Boulay's publications referencing list 

 The ultimate numbers and the 3/2 ratio

Jean-Yves Boulay. The ultimate numbers and the 3/2 ratio. 2020. ⟨hal-02508414v2⟩

https://hal.archives-ouvertes.fr/hal-02508414v2

Abstract : According to a new mathematical definition, whole numbers are divided into two sets, one of which is the merger of the sequence of prime numbers and numbers zero and one. Three other definitions, deduced from this first, subdivide the set of whole numbers into four classes of numbers with own and unique arithmetic properties. The geometric distribution of these different types of whole numbers, in various closed matrices, is organized into exact value ratios to 3/2 or 1/1.

Résumé : Selon une nouvelle définition mathématique, les nombres entiers naturels se divisent en deux ensembles dont l'un est la fusion de la suite des nombres premiers et des nombres zéro et un. Trois autres définitions, déduites de cette première, subdivisent l'ensemble des nombres entiers naturels en quatre classes de nombres aux propriétés arithmétiques propres et uniques. La distribution géométrique de ces différents types d'entiers naturels, dans de diverses matrices fermées, s'organise en ratios exacts de valeur 3/2 ou 1/1.

https://www.researchgate.net/publication/339943634_The_ultimate_numbers_and_the_32_ratio

10.13140/RG.2.2.32843.34081/2

 New Whole Numbers Classification

Jean-Yves Boulay. New Whole Numbers Classification. 2020. ⟨hal-02867134⟩

https://hal.archives-ouvertes.fr/hal-02867134

Abstract : According to new mathematical definitions, the set (ℕ) of whole numbers is subdivided into four subsets (classes of numbers), one of which is the fusion of the sequence of prime numbers and numbers zero and one. This subset, at the first level of complexity, is called the set of ultimate numbers. Three other subsets, of progressive level of complexity, are defined since the initial definition isolating the ultimate numbers and the non-ultimate numbers inside the set ℕ. The interactivity of these four classes of whole numbers generates singular arithmetic arrangements in their initial distribution, including exact 3/2 or 1/1 value ratios.

Résumé : Selon de nouvelles définitions mathématiques, l’ensemble (ℕ) des nombres entiers naturels se subdivisent en quatre sous ensembles (classes de nombres) dont l’un est la fusion de la suite des nombres premiers et des nombres zéro et un. Ce sous ensemble, de premier niveau de complexité, est nommé l’ensemble des nombres ultimes. Trois autres sous ensembles, de niveau progressif de complexité, sont définis depuis la définition initiale isolant les nombres ultimes et les nombres non ultimes à l’intérieur de l’ensemble ℕ. L’interactivité de ces quatre classes de nombres entiers naturels génère des arrangements arithmétiques singuliers dans leur distribution initiale dont d’exacts ratios de valeur 3/2 ou 1/1.

https://www.researchgate.net/publication/341787835_New_Whole_Numbers_Classification

10.13140/RG.2.2.26139.90402/1

 Genetic code, quantum physics and the 3/2 ratio

Jean-Yves Boulay. Genetic code, quantum physics and the 3/2 ratio. 2020. ⟨hal-02902700⟩

https://hal.archives-ouvertes.fr/hal-02902700

Abstract : The analysis of the quantum structure of the five chemical elements composing the coded twenty amino acids and the four coding nucleotides of DNA working in the organization of the genetic code reveals an opposition of their respective constituents in always an arithmetic ratio of value 3/2 according to the parity of the number of their quantum shells. Also, the quantum analysis of the amino acid Glycine, the smallest component of peptides that can be confused with saturated base, reveals the same arithmetic oppositions of 3/2 value of its components by the differentiation, operated according to their number of protons, of its five chemical groups. In sidelines to this study, a new graphic representation of the chemical elements is introduced: chevron form quantum chart.

Résumé : L’analyse de la structure quantique des cinq éléments chimiques composant les vingt acides aminés codés et les quatre nucléotides codant d’ADN œuvrant dans l’organisation du code génétique révèle une opposition de leurs constituants respectifs en toujours un ratio arithmétique de valeur 3/2 selon la parité du nombre de leur couche quantiques. Aussi, l’analyse quantique de l’acide aminé Glycine, plus petit composant des peptides pouvant être confondu en base saturée, révèle les mêmes oppositions arithmétiques de valeur 3/2 de ses composants par la différenciation de ses cinq groupes chimiques opérée selon leur nombre de protons. En marge de cette étude, une nouvelle représentation graphique des éléments chimiques est introduite : les diagrammes quantiques en forme de chevron.

https://www.researchgate.net/publication/343064455_Genetic_code_quantum_physics_and_the_32_ratio

 DOI :  10.13140/RG.2.2.26505.67681/3

 Chevron Form Quantum Charts

New graphical representation of quantum orbitals

Jean-Yves Boulay. Chevron Form Quantum Charts: New graphical representation of quantum orbitals. 2020. ⟨hal-03018374⟩

https://hal.archives-ouvertes.fr/hal-03018374

Abstract: It is proposed here to represent the quantum distribution of atomic orbitals in an unprecedented table where the quantum shells and subshells are drawn in the form of chevrons whose vertices are occupied by orbitals with the magnetic quantum number m = 0. This new representation visually shows, much better than a classic linear chart, the relationship between the number of quantum shells and the number of orbitals . Also, this new visual model can be easily used in the individual quantum depiction of the atoms represented alone or into molecules and can find its place in illustration of some two-dimensional space-time quantum theories. Finally, this graphic representation allows to introduce the hypothesis of the existence of stealth orbitals, quantum gates opening towards singularities.

Résumé : Il est proposé ici de représenter la distribution quantique des orbitales atomiques dans un tableau inédit où les couches et sous-couches quantiques sont dessinées sous forme de chevrons dont les sommets sont occupés par des orbitales avec le nombre quantique magnétique m = 0. Cette nouvelle représentation montre visuellement, bien mieux qu'un graphique linéaire classique, la relation entre le nombre de couches quantiques et le nombre d'orbitales. En outre, ce nouveau modèle visuel peut être facilement utilisé dans la représentation quantique individuelle des atomes représentés seuls ou en molécules et peut trouver sa place dans l'illustration de certaines théories quantiques spatio-temporelles bidimensionnelles. Enfin, cette représentation graphique permet d'introduire l'hypothèse de l'existence d'orbitales furtives, portes quantiques ouvrant vers des singularités.

https://www.researchgate.net/publication/346080523_Chevron_Form_Quantum_Charts

DOI : 10.13140/RG.2.2.35925.45283

Jean-Yves BOULAY independent researcher (without affiliation) – FRANCE

e-mail: jean-yvesboulay@orange.fr - https://orcid.org/0000-0001-5636-2375

New quantum chart : The chevron form quantum chart

The quantum study of the genetic code is an opportunity to propose a new type of table describing the quantum organization of atoms. In this chart, illustrated below, the different quantum shells and subshells are presented in the form of chevrons. At the top end of each rafter are indicated the names of the different shells and subsells; at the left end of these chevrons, the numbers of orbitals and electrons of these different shells and quantum subshells are indicated. At each chevron vertex is the orbital where the quantum number m = 0. The orbitals with positive quantum number m are progressively positioned towards the top of these chevron vertices and the orbitals with negative quantum number m are progressively positioned towards the outside left of these chevron vertices.

This new graphic design is more explicit in describing the quantum structure of atomic elements than any other usual linear chart. Very visually, this chevron configuration clearly highlights the arithmetic progression of the orbital numbers of the different quantum shells in square powers of the level of these electronic shells:

- 1^st shell →           1² = 1 orbital,

- 2^nd shell →          2² = 4 orbitals,

- 3^rd shell →          3² = 9 orbitals,

- 4^th shell →          4² = 16 orbitals, etc.

In this table, and more generally in the quantum study of the atomic elements, the electronic spin is not detailed (by ascending or descending arrows). In return, it is the migratory or non-migratory nature of the electrons that is the subject of study. Thus, for example, the representation of the nitrogen atom such as that illustrated below is favoured.

Moving illustration of the concept of new quantum chart in chevron form 

You can use these images with please reference of the author and this paper: 

Jean-Yves Boulay. Genetic code, quantum physics and the 3/2 ratio. 2020. ⟨hal-02902700v3⟩

New: new paper about chevron form quantum charts